Lt. Bob said:
The D/A does the converting of bits to analog right?
And it takes those samples , individual specific moments of time along the waveform, and reconstructs the original waveform. I've also read that some early poorly designed converters could have errors as severe as even playing wrong pitches.
Now .... there are many many places along that waveform that it didn't sample and it has to fill in the blanks so to speak.
But doesn't that mean it has to, for instance, that the overall wave is a sinewave?
What if it isn't?
I've never heard of a converter that got the pitches wrong. To me that would indicate that a sample rate was out of sync, maybe trying to play a 44.1 file at 48 (which I've done before - my bad...) or else the clock was defective.
As for the shape of the sine wave, it's pretty much a pure tone with no distortion. I chose that for the examples I posted to try to get the limitations of the file format to distort the wave so it would be readily apparent and highly visible. Presumably if you can get a pure tone with no distortion to not distort, the bit depth should be sufficient to not worry about. It might also be dependant on the frequency of the wave - lower ones take longer to develop.
How do I get there?
For us to hear anything we need something to vibrate. If it vibrates fast enough, say 20 cycles per second, this is the bottom threshold where we can hear a pitch. This is the horizontal axis of the sound sampler, determined by sample rate. Assuming a rate of 44.1 kHz (it really doesn't matter so much) a lot of the accuracy of the sound has to do with the vertical axis which is going to give the sound enough power or volume for us to hear the vibration. The shape of what happens on the vertical axis doesn't affect the speed of how it oscillates. If we hear 440 cycles per second as a sine wave, it's an A note. If we hear 440 cycles per second of a badly distorted sine wave, it's still an A note.
When there's something that happens where it didn't sample, it's the vertical axis, or the bit rate at fault that causes distortion. If we can get the horizontal AND vertical axes to line up properly to the input signal, the sound should come back clean.
Relatively.
Put it this way, the scale of sample rate should be sufficient to capture the upper limit of frequencies you want to capture. After that it's up to the bit rate.
With PCM encoding using linear quantization, the "linear" part (this is for PCM intended for audio recording) means equal step size.
The A/D converter reads the voltage coming in and assigns it a value depending on its amplitude and polarity. This gets coded to a binary number. The D/A takes the number and converts it back into voltage.
We know that each bit operates on 6 dB of range. 16 bit gives 96 dB range. 24 bit gives 144 dB range.
The voltage steps from the A/D that get converted into binary place markers are all an equal fraction of a volt.
If we want a relative 6 dB increase we have to double the voltage. If we want a relative 6 dB decrease we have to cut the voltage in half.
So at 0 dBfs in 16 bit, we have 65,532 levels to quantize the strength of the signal. At -6 dBfs we have 32,766 levels. Effectively we can sample to very, very minute fractions of time and power within this range so the resolution or accuracy should be very good. The system should be able to handle changes in level much better than our ears can.
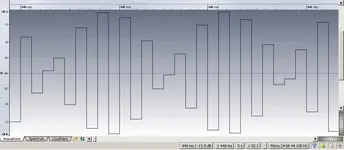
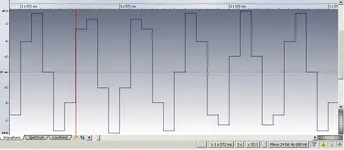
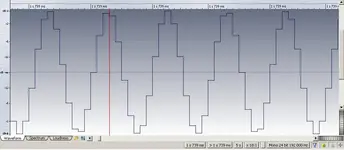
The resolution cuts in half every time we reduce the thing by 6 dB. On a simple sine wave test it started to fall apart for me at -60 dBfs at 16 bit with a 440 cycle wave. This is having the system operate on around 6 bits, or 64 discreet quantization levels. Approximately, anyway. The errors start coming in where the A/D starts to get values like say 30.98, 31.65, 31.79, 31.93, 32.06, 31.94, 31.8, 31.66, 30.97.
PCM stores the numbers as 30, 31, 31, 31, 32, 31, 31, 31, 30. Regardless of the shape of the wave, the numbers are close, the frequency is correct and the result is distortion. For practical purposes this is only going to concern someone recording the most dramatic, dynamic, uncompressed symphonic performance.
24 bit resolution can help because it parks most of the junk at the extreme bottom beyond the reach of preamps, mics, amps, speakers and ears. -60 dBfs just became 14 bit audio instead of 6 bit.
Does this make any sense?