crazydoc
Master Baiter
Would you believe two for stereo and one to take apart?
And I had a little extra money in the amount I'd negotiated with my wife, enough for another pre or two more mics. I decided on the mics (another 300 and another 900.)
And I had a little extra money in the amount I'd negotiated with my wife, enough for another pre or two more mics. I decided on the mics (another 300 and another 900.)
Marik
Pro Microphone Design
Nah, waisted time. Ribbon mics sonic qualities are very much due to their acoustical enviroment. By shorting one ribbon you just lose 6 db of signal, while acoustically, it will be pretty much the same thing. It is better to leave it as it is.
Not to get confused, this is a technical nonsense and is just wrong information. I already asked Mr. Joly to comment and provide proof, but apparently he ignored it.
Best, M
Last edited:
dgatwood
is out. Leave a message.
Yeah, pretty much, except it would have to be in a double pole configuration.
dgatwood
is out. Leave a message.
The roll-off, yes, but AFAIK, the off-axis coloration is largely caused by having two elements slightly out of phase in terms of when the sound arrives.
Marik
Pro Microphone Design
Yeah, another nonsense from the same source. I am not sure why that particular individual is trying on numerous boards and numerous occasions to fool people with some technical terms, without any understanding or knowledge behind them. Or is it supposed to sound "impressive" and show how "smart" he is?
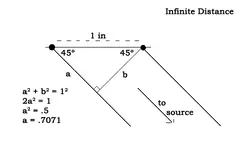
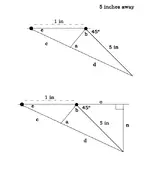
Let's see, what is the distance between ribbon elements? 1 inch? So the correspoinding frequency will be 13.5KHz. Say, effect starts being noticalble starting from half wavelength, i.e. 6.75KHz.
As already was said in another thread, the on-axis frequency response in those double ribbons starts rolling off @ 4KHz, so off-axis will be affected even sooner.
Doesn't 6.75KHz look like it is already way out of off-axis bandwidth?
In fact, if anything, it will affect rather on-axis response, but this is already topic for completely different discussion...
But if you want to experiment--by all means. Make the "jumper" out of very thick wire, so you don't get additional copper noise.
Best, M
Last edited:
D
drBill
New member
I don't want this to turn into a pissing contest, but I do know that if I have 2 mics on a source and pull one back and inch, I'll start to get phasing elements when combining that are for the most part undesireable.
crazydoc
Master Baiter
Double post
crazydoc
Master Baiter
Not what you specified - but you could use two toggle switches in parallel and mechanically link the lever arms - might be a little more pricey though.
Or you could get Part# 1223 or 1224 here:
http://www.stewmac.com/shop/Electro..._Switches_and_knobs/Mini_Toggle_Switches.html
D
drBill
New member
FYI, from the other thread: Chance used the ACM200 on what he previously described as "a thin vocal" IIRC - Track number 2 in the link below. Doesn't sound too thin anymore. 
Kinda phasey though, but I'm going to guess that's due to the mp3.
Kinda phasey though, but I'm going to guess that's due to the mp3.
C
chance
Well-known member
That phasiness might be the doubled vox
D
drBill
New member
Chance, I'm hearing it in the piano as well....
The vocal sounded good tone wise. I think the mic must have really helped out with her voice. It didn't sound thin to me at all.
bp
The vocal sounded good tone wise. I think the mic must have really helped out with her voice. It didn't sound thin to me at all.
bp
dgatwood
is out. Leave a message.
I don't quite understand your response. There should be no audible effect from phase differences on axis because the sound will arrive at both ribbons at the same time, thus the timing differences would put any distortion well outside the human hearing range up to a few degrees off axis.
At 90 degrees, 6.7 kHz would be 180 degrees out of phase, and thus would be completely nulled out. This is, of course, the unimportant case because everything should already nulled out by the ribbon, give or take.
The question then becomes how it behaves between those two extremes. To some extent, any mic is going to be more directional at higher frequencies, so you will have less off-axis response in the high end. However, what response there is will still have that artificial null, and the farther off axis, the more likely you are to have response above and below that null that will make it sound odd.
In addition to the null, if you have anything other than a pure sine wave, you will probably also see points of constructive interference causing false overtones. Say you have a sawtooth wave and one is shifted 90 degrees out of phase, you end up with a signal at twice the frequency. Shift by other values and you can get all sorts of fun overtones.
I just don't buy that there's not any appreciable response at 6.7 kHz off axis unless you're right in the 90 degree null. If Michael Joly's numbers are even remotely in the ballpart, 6 dB per octave would mean that 6.7 would be down somewhere around 4.5 dB-ish. Having a complete hole at that frequency, therefore, would be very noticeable, and you'd start hearing distortion at a much lower frequency than that as you approach the null from either side.
The most critical problem, though, is that the frequency of the null sweeps from infinity down to about 6.5 kHz depending on your position, and as a result, as you move around, the sound quality would change far more than would normally be the case with a single ribbon of identical construction.
Am I missing something?
Marik
Pro Microphone Design
Don't forget the half wavelength of 6.75KHz is the worst case, and as you rightly noticed will happened at 90* null.
At 45* because of directivity the HF signal will be already roughly -5db down. At the same time make a simple vector calculation to see that the full wavelength will be already not 1", but twice less, translating into twice higher frequency, so the number will be something like 15.5db-ish.
You will need to give me hard numbers to convince it will affect the sound in any major way.
Best, M
P.S. As a side note, because of cavity resonances and diffractions there will be no complete hole (anywhere
)
Last edited:
dgatwood
is out. Leave a message.
Don't forget the half wavelength of 6.75KHz is the worst case, and as you rightly noticed will happened at 90* null.
At 45* because of directivity the HF signal will be already roughly -5db down. At the same time make a simple vector calculation to see that the full wavelength will be already not 1", but twice less, translating into twice higher frequency, so the number will be something like 15.5db-ish.
You will need to give me hard numbers to convince it will affect the sound in any major way.
Best, M
P.S. As a side note, because of cavity resonances and diffractions there will be no complete hole (anywhere
Fair enough. There's no such thing as complete cancellation in the real world, period. Even mixing the + and - sides of a microphone's output together will usually generate a little signal....
That said, my math doesn't agree with your math. At 45 degrees, assuming infinite distance to make the math easier (~45 degrees to each capsule), if you draw two 45 degree slants to two points on the same line, then draw a 90 degree perpendicular to the longer line that intersects with the point at the end of the shorter line, you have a right triangle whose hypotenuse is 1 inch, so each side is 0.707106781 inches. That's the effective difference in distance between the two capsules for that source. Based on that, the out of phase point is half of 19 kHz ,or 9.5 kHz. You would otherwise be down say 10 dB but instead are down to (effectively) nothing.
Of course, that assumption about infinite distance is a little bit unrealistic. The closer you get to the mic, assuming you pin the closer capsule at 45 degrees, the more acute the angle to the more distant capsule gets, and the longer that side of this imaginary triangle gets, thus the greater the effective distance between capsules. For example, at five inches, if you are 45 degrees to the closer capsule, you are at about 30 degrees to the farther capsule. After a lot of ugly trig, the additional distance to the second capsule is up to about .866 inches, so the null is at half of 15.4 kHz, or 7.7 kHz. If it were straight on, with a single ribbon, that should be down less than 6dB, but with the double it should be mostly nulled out.
If you pin the distant capsule at 45 degrees instead of the closer one, then move to five inches from the capsule, I still get .6 inches of difference. It doesn't hit half an inch until the source is about 2.516 inches from the nearest capsule. (Ugh, arctangents.)
Of course, this assumes an omnidirectional source. I won't even try if we don't make that assumption.
Marik
Pro Microphone Design
Sorry, I was way too lazy to make ANY math
The "null" will be not @ 7.7KHz, but @ 15.4KHz.
dgatwood
is out. Leave a message.
Sorry, I was way too lazy to make ANY math
The "null" will be not @ 7.7KHz, but @ 15.4KHz.
I'm not following the logic there. If the wavelength of the delay corresponds with 15.4 kHz, then a signal at 15.4 kHz delayed by that distance would be delayed by a full wavelength, which means it would be constructive interference, just one cycle delayed. That's where the second full-strength peak would be in a spectrum map, not the first trough.
You get destructive interference when a signal is delayed by a half cycle (or any odd multiple of half cycles, e.g. 3/2 cycles, 5/2 cycles, ...), thus putting it 180 degrees out of phase with the original signal. It is delayed 1/2 cycle if the wavelength is twice as long as a 15.4 kHz wave, which means the frequency is half as high. Thus, the first trough in a spectrum map would be at 7.7 kHz, not 15.4 kHz.
(The second trough, at a whopping 23.1 kHz, would basically be outside the human hearing range, though it might start rolling off within the upper extremes of human hearing... not that the mic will pick much up at those frequencies anyway, though....)
D
drBill
New member
I'm getting a headache......
dgatwood
is out. Leave a message.
I'm getting a headache......
I wish I could draw pictures freehand directly on the web. It would make the discussion far more intelligible. Okay, here's the infinite distance case. Treat the ribbons as a single point in space marked by the black dots. The important value is "a". If the sound travels from an infinitely distant point, it arrives at the rightmost ribbon at the same time as it arrives at every point along line b, so the distance from line b to the leftmost dot (the length of line a) is the time delay for the left ribbon.
We know a = b because it is a right triangle and the opposite angles are the same. I could also have calculated this as sin(45 degrees) = a / hypotenuse, and since the hypotenuse is 1, a = sin(45 degrees).
- sine of an angle = length of opposite side / length of hypotenuse; for the left 45 degree angle, the opposite is b, hypotenuse is 1.
- cosine of the angle is length of adjacent side over the hypotenuse; for the left 45 degree angle, the adjacent is a, hypotenuse is 1.
- tangent is opposite over adjacent; for the left 45 degree angle, the opposite is b, adjacent is a.
The arc versions go in the opposite direction, so if you know the opposite and adjacent, you can divide the opposite over the adjacent and take the arctangent of that fraction and you'll get the angle.
Attachments
D
drBill
New member
Now I've got a migrain.......
Must.......lay..........down.
Or maybe just put up a mic and make some music.
dgatwood
is out. Leave a message.
Actually, I think my math may have been slightly off. I'm recomputing everything. based on 5 inches instead of trying to go from 45 and 30 degree angles and calculate the distance, so none of these numbers will match what I did before, and that is intentional. However, I think I might have used a right triangle on one of my two calculations earlier where I should have used an isosceles triangle.... My bad. I think the numbers are probably within about 10% of the right values, but I'm not going to bother to recompute the original numbers. We'll just call them "close enough".
We know that a and b are equal in the first part. We need to calculate the length c. To begin, we need to figure out... a lot of things. Start by figuring out the total length of the line containing segment c. To do this, look at the second image.
sin(45 degrees) = n / 5
n = 5 * sin(45 degrees) = 3.53553391 inches
Again, because this is a right triangle and the angles are 45 and 45, we know that o = n.
Thus, pythagorean theorem time.
(3.5355 ^2) + ((1 + 3.5355) ^2) = ((c + d) ^2)
c + d = 5.75 inches, give or take.
Since a = b, d = 5 inches. Thus, c = .75 inches.
And if anybody cares about angle e, we can calculate that with the larger right triangle as well. The tangent of angle e is (n / (o+1)), which would mean e is arctan(3.5355 / 4.5355), or about 37.93 degrees.
We know that a and b are equal in the first part. We need to calculate the length c. To begin, we need to figure out... a lot of things. Start by figuring out the total length of the line containing segment c. To do this, look at the second image.
sin(45 degrees) = n / 5
n = 5 * sin(45 degrees) = 3.53553391 inches
Again, because this is a right triangle and the angles are 45 and 45, we know that o = n.
Thus, pythagorean theorem time.
(3.5355 ^2) + ((1 + 3.5355) ^2) = ((c + d) ^2)
c + d = 5.75 inches, give or take.
Since a = b, d = 5 inches. Thus, c = .75 inches.
And if anybody cares about angle e, we can calculate that with the larger right triangle as well. The tangent of angle e is (n / (o+1)), which would mean e is arctan(3.5355 / 4.5355), or about 37.93 degrees.
Attachments
Last edited: