Toddskins
Member
Let's face it. We're the guys who take sound design to the nth level. I need your collaboration for a feat that is not faint-hearted, I think.
For 25 years, I have imagined creating 3-D sound, in a way that has not been done, at least to my knowledge.
Thank God I own a Kurzweil K-series that has numerous mathematical models that can be incorporated into the design signal, so I am fairly certain that if you guys can help me with the algorithm, I'll be able to implement it in my keyboard signal.
Ok.
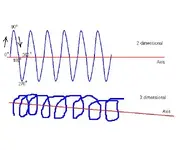
Here's the scoop: Imagine a toy slinky, stretched out in front of your face, horizontally, like a pipe, moving from left to right. See uploaded image below.
For starters, I'm wishing to create a swirling sound that spins, and then moves left to right through the sound field. The variables I am pretty sure that will be varied will be 1) amplitude, 2) panning, 3) maybe a little pitch, similar to a doppler effect, and then probably some type of reverb room. From what I have read about 3-D sound, various companies have utilized phase variance (I'm not 100% sure what that would mean).
I've found this great starting point that not only gives some good evaluation, but there are a couple of great 3-D sound examples at the bottom of the page, listed under [External Links]. By all means, be sure to put your HEADPHONES on. The best example is the "Virtual Barbershop"! Listen to it now! Then come back here.
http://en.wikipedia.org/wiki/3D_audio_effect
After you have listened to that, and taken a look at the definition on that site, can you offer some input to me on how I could design the algorithm into my Kurzweil's signal path, so that when people listen with headphones, they would feel/hear the effect of 3-D sound going through and around their head?
I'm wondering, as you look at the illustration of the slinky (imagine 3 dimensional), what do those oscillating circles, along the moving slinky path, look like in 2 dimensions? I have held up a spiral notebook to the light, to try and see what that looks like in 2-D, and it seems to look like triangle waveforms. [See image below]
So, the amplitude (loudness) would be greatest at 0 degrees, and as the sound moves up the cycle to 90 degrees, the sound gets less loud, and is at its minimum loudness when it reaches 180 degree. Then, the sound begins to return toward you, as it continues moving through the cycle toward 270 degrees, and is loudest again at 360 degrees.
But to simulate 3-D sound, the speed cannot be linear. So in the 2-Dimensional triangular waveform, would not the sound seem to take longer to move along various points of the waveform?
Taking the doppler effect into account, would the pitch diminish ever so slightly as the sound moves away from you, and rise as it returns?
I will be thrilled if you guys can help me figure this thing out. Afterwards, I would love to experiment with moving the whole axis, like as if the sound were going directly through the centers of your ears. And then, move the axis vertical, right through your head from top to bottom, to simulate a tornado.
Lastly, there must be a way to also simulate height and depth positioning.
Please, let's put our engineering caps on and help me with this!
Thanks in advance!
Todd
For 25 years, I have imagined creating 3-D sound, in a way that has not been done, at least to my knowledge.
Thank God I own a Kurzweil K-series that has numerous mathematical models that can be incorporated into the design signal, so I am fairly certain that if you guys can help me with the algorithm, I'll be able to implement it in my keyboard signal.
Ok.
Here's the scoop: Imagine a toy slinky, stretched out in front of your face, horizontally, like a pipe, moving from left to right. See uploaded image below.
For starters, I'm wishing to create a swirling sound that spins, and then moves left to right through the sound field. The variables I am pretty sure that will be varied will be 1) amplitude, 2) panning, 3) maybe a little pitch, similar to a doppler effect, and then probably some type of reverb room. From what I have read about 3-D sound, various companies have utilized phase variance (I'm not 100% sure what that would mean).
I've found this great starting point that not only gives some good evaluation, but there are a couple of great 3-D sound examples at the bottom of the page, listed under [External Links]. By all means, be sure to put your HEADPHONES on. The best example is the "Virtual Barbershop"! Listen to it now! Then come back here.
http://en.wikipedia.org/wiki/3D_audio_effect
After you have listened to that, and taken a look at the definition on that site, can you offer some input to me on how I could design the algorithm into my Kurzweil's signal path, so that when people listen with headphones, they would feel/hear the effect of 3-D sound going through and around their head?
I'm wondering, as you look at the illustration of the slinky (imagine 3 dimensional), what do those oscillating circles, along the moving slinky path, look like in 2 dimensions? I have held up a spiral notebook to the light, to try and see what that looks like in 2-D, and it seems to look like triangle waveforms. [See image below]
So, the amplitude (loudness) would be greatest at 0 degrees, and as the sound moves up the cycle to 90 degrees, the sound gets less loud, and is at its minimum loudness when it reaches 180 degree. Then, the sound begins to return toward you, as it continues moving through the cycle toward 270 degrees, and is loudest again at 360 degrees.
But to simulate 3-D sound, the speed cannot be linear. So in the 2-Dimensional triangular waveform, would not the sound seem to take longer to move along various points of the waveform?
Taking the doppler effect into account, would the pitch diminish ever so slightly as the sound moves away from you, and rise as it returns?
I will be thrilled if you guys can help me figure this thing out. Afterwards, I would love to experiment with moving the whole axis, like as if the sound were going directly through the centers of your ears. And then, move the axis vertical, right through your head from top to bottom, to simulate a tornado.
Lastly, there must be a way to also simulate height and depth positioning.
Please, let's put our engineering caps on and help me with this!
Thanks in advance!
Todd