Do I understand "Q"?

[RAMI]

This is how I think it goes. Please, someone correct me if I'm off.

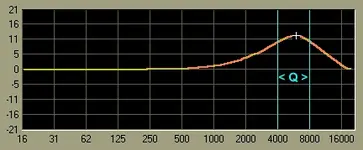
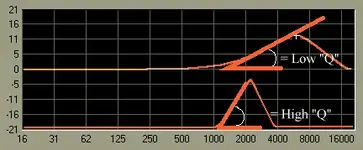
If you have a "Q=1": highest freq.-lowest freq.=middle freq.
So if I'm cutting 600hz with a Q of 1, the highest freq. I'm affecting is 900hz, and the lowest is 300hz (900-300=600).


If you have a "Q=2": highest freq.-lowest freq=1/2 of middle freq.
So if I'm cutting 600hz with a Q of 2, the highest freq. I'm affecting is 750hz, and the lowest is 450hz (750-450=300...1/2 of 600).


If you have a "Q=4": highest freq.-lowest freq=1/4 of middle freq.
So if I'm cutting 600hz with a Q of 4, the highest freq. I'm affecting is 675hz, and the lowest is 525hz (675-525=150...1/4 of 600).

And so on.....

Is this right?

 

[Tonio]

Of course it depends on what you are using, but in a para eq wether hardware or software, it would depend on the manufactures spec(the upper /lower point of bell bandwidth).
I would put up to say that Q is the bandwidth of the frequencies you are cutting or boosting. Q is the center frequency, the value is the bandwidth.
high valueQ= narrow bandwidth
low value Q= wide bandwidth
Normally 1.4 Q is an octave.

For boosting a use a wide(-1.4)Q to bring up the goodies. For cutting narrow(lowvalue+1.4)Q to cut out the crapness-find the offending frequency but get narrow as can, then cut.

Thats what I understand is the way its supposed to be, but some DAW's may have it bassackwards.

T

 

[Dogman]

I think you have it pretty close man...I just know that the larger the number in my eq, it narrows the bandwidth it affects.

 

[SouthSIDE Glen]

The calculations you guys give are basically correct, but it gets a bit trickeir than that.

Q typically does not refer to the entire width of the bell curve*, but rather the center width of the curve bordered on either side of the center frequency by the points where the curve drops or gains 3dB (depending on whether you're boosting or cutting) from the gain level at the center frequency. So if one has a Q of an octave (typically Q=1.5, though I hate Q numbers and prefer to refer to octave widths myself)

The tricky thing about that definition, is that technically means that when one is cutting or boosting by less than 3dB, the value for Q would be infinite, and in fact would change as one moved beyond the 3dB mark if the shape of the curve were constant as it is in graphic EQs and so-called "constant Q" EQs. For this reason, most parametric EQs are "variable Q" EQs; they change the shape of the curve (often to non-bell shapes) dynamically as the amount of gain changes. The Q actually dynamically changes with gain.

It's this shape given to the curve that Q is really defining, and (technically speaking), not necessarily the bandwidth, as the bandwidth varies with gain.

In summary: fuggedaboutit! Just work with octave values, as that's what matters musically, and also doesn't change meaning with gain value.

G.

*In fact, in theory, standard bell curves are infinite in width since they never actually reach a value of zero.

 

[RAMI]

Thanx for the explanations. So I basically had it right as far as my calculations, no? I find it easier to do that equation than to work with octaves. That's just a testament to my ignorance of octaves, not a comment on doing it that way.

 

[mshilarious]

Thanx for the explanations. So I basically had it right as far as my calculations, no? I find it easier to do that equation than to work with octaves. That's just a testament to my ignorance of octaves, not a comment on doing it that way.

It was close but you didn't account for the logarithmic nature of octaves and frequencies. So in your first example, 300/600/1200 would be more accurate (with a Q of 1.5 as Glen pointed out).

I like the dB/octave control on the UAD Precision EQ. That's very straightforward

 

[SouthSIDE Glen]

Thanx for the explanations. So I basically had it right as far as my calculations, no?

Yes and no. While the math is correct, the conclusions are generalized, at best. When you say "I'm affecting 900hz", with many EQs you are really technically affecting more than than 900Hz, because the Q value is not necessarily referring to the entire curve, just to the central main "tenderloin" of the curve.

G.

 

[Dogman]

Yes and no. While the math is correct, the conclusions are generalized, at best. When you say "I'm affecting 900hz", with many EQs you are really technically affecting more than than 900Hz, because the Q value is not necessarily referring to the entire curve, just to the central main "tenderloin" of the curve.

G.

Ahh...so even though it appears to "end" at 900, it is just so small we don't see it on our screens, but in reality, it's probably still affecting, roughly half a db...or something to that matter.....

 

[SouthSIDE Glen]

Ahh...so even though it appears to "end" at 900, it is just so small we don't see it on our screens, but in reality, it's probably still affecting, roughly half a db...or something to that matter.....

It can often be much more than that.

Let's say the manufacturer is using the standard Q definition of the part of the curve that is +/- 3dB from the gain of the center frequency. The attached graph is the response curve of a EQ setting centered on 6khz with a Q of 1.5 (one octave). The light blue lines represent the Q "boundaries". All parts of the orange curve outside of the Q boundaries represent signifigant frequency boosts outside of those boundaries.

I borrowed this graph and added the Q marking myself from this wonderful discourse on EQ by Lionel Drummond on the ProRec website. I hope he doesn't mind my marking it up in return for sending all you guys and gals to go read his article.

G.

 

[RAMI]

WOW! I didn't realise it can fall that far out of the "boundaries". Thanx for the info in this post to all of you. I guess my formula was a little too cut and dry.

 

[Dogman]

Thanks G. I never really eq by looking at something, but I know the graphics are there to help you get an idea of where you are at. Never really thought about what all you were affecting. Seems there is always more for us to learn.....

 

[Dogman]

WOW! I didn't realise it can fall that far out of the "boundaries". Thanx for the info in this post to all of you. I guess my formula was a little too cut and dry.

Cut and dry, but very close to what some of us see. And again, it always comes down to "what sounds good".....

 

[SouthSIDE Glen]

Yeah, it's easy for us to think of "Q" as meaning (more or less) "the total width of the curve". But that's not what it really means at all. It's just a type of measurement for defining the nature of the curve without directly ID'ing it's total size.

G.

 

[RAMI]

Yeah, it's easy for us to think of "Q" as meaning (more or less) "the total width of the curve". But that's not what it really means at all. It's just a type of measurement for defining the nature of the curve without directly ID'ing it's total size.

G.

Those bastards!!!

 

[RAMI]

It can often be much more than that.

Let's say the manufacturer is using the standard Q definition of the part of the curve that is +/- 3dB from the gain of the center frequency. The attached graph is the response curve of a EQ setting centered on 6khz with a Q of 1.5 (one octave). The light blue lines represent the Q "boundaries". All parts of the orange curve outside of the Q boundaries represent signifigant frequency boosts outside of those boundaries.

I borrowed this graph and added the Q marking myself from this wonderful discourse on EQ by Lionel Drummond on the ProRec website. I hope he doesn't mind my marking it up in return for sending all you guys and gals to go read his article.

G.

Ok, now I'm just nit-picking for the sake of discussion, not trying to keep pushing my little "equation". But in your example, I just noticed that you said the "Q" is 1.5. But in my "calculations", the "Q" has to be 1 for the bell to stay between 3k and 9k. I'm not saying it will, but I wonder how much closer to the supposed boundaries it would be with a "Q" of 1.
But I also realise, after reading your posts and MSHILARIOUS's explanation that there are other factors I'm not taking into account.

 

[Harvey Gerst]

For some people, it might be easier to visualize "Q" as an angle, like this:

 

[boingoman]

The tricky thing about that definition, is that technically means that when one is cutting or boosting by less than 3dB, the value for Q would be infinite, and in fact would change as one moved beyond the 3dB mark if the shape of the curve were constant as it is in graphic EQs and so-called "constant Q" EQs. For this reason, most parametric EQs are "variable Q" EQs; they change the shape of the curve (often to non-bell shapes) dynamically as the amount of gain changes. The Q actually dynamically changes with gain.
.[/SIZE]

I think it's more correct to say parametrics have adjustable, not variable.

Because constant vs. variable Q is a description of function. It's actually constant-Q eqs that vary the shape of the curve by design, so that their Q factor remains constant during small amounts of boost. Variable-Q eqs have the behavior you described, ie at small amounts of boost/cut (less than 3db) the bandwidth affected is much wider than at higher boost/cut settings.

 

[SouthSIDE Glen]

Ok, now I'm just nit-picking for the sake of discussion, not trying to keep pushing my little "equation". But in your example, I just noticed that you said the "Q" is 1.5. But in my "calculations", the "Q" has to be 1 for the bell to stay between 3k and 9k. I'm not saying it will, but I wonder how much closer to the supposed boundaries it would be with a "Q" of 1.
But I also realise, after reading your posts and MSHILARIOUS's explanation that there are other factors I'm not taking into account.

Again, the key is to remember that the area the Q "covers" is defined by +/- 3dB from the center frequency gain. Therefore the relation of the "Q width" to "bell width" changes depending upon the amount of boost/cut. That graph represented a case of +12dB boost.

By technical definition, the curve of a 2dB boost would have infinitely wide Q boundaries. An EQ boosted or cut by 24dB (if such an EQ existed) would have an even narrower "Q-to-bell" ratio.

Q is nothing but a way of measuring the steepness of the slope of the curve. Using the same bell-type equation, there is only one curve that will fit the three points on a graph represented by the centerpoint (the gain at center frequency) and the two points represented by the delta 3dB points on either side of it. The makers of "Q" could have just as easily picked +/- 5dB as the points. There are probably some good reasons they picked 3dB, but for purposes of this description trying to relate it to bell width and trying to use the Q boundaries to relate to what frequencies the EQ is actually affecting, the 3dB points on the curve are meaningless and arbitrary.

It's a fine point to put to words, but while Q is an indication of bell width by way of the fact that it actually defines the sharpness of curve slope, it is not a direct measure of bell width. The bell cuves will always extend beyond the Q points on any curve greater than +/-3dB and will fall to zero or near zero inside of the Q boundaries on any curve less than +/3dB.

G.

 

[boingoman]

There are probably some good reasons they picked 3dB, but for purposes of this description trying to relate it to bell width and trying to use the Q boundaries to relate to what frequencies the EQ is actually affecting, the 3dB points on the curve are meaningless and arbitrary.
.

Sort of arbitrary. +/- 3b= twice or half the power.


-edited